Recent Posts
- AI for the Research Ecosystem workshop #AI4RE – round up 30 March 2024
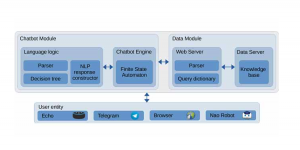
- Integrating Conversational Agents and Knowledge Graphs Within the Scholarly Domain 18 March 2023
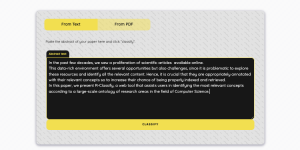
- R-Classify: Extracting Research Papers’ Relevant Concepts from a Controlled Vocabulary 12 November 2022
- Leveraging Knowledge Graph Technologies to Assess Journals and Conferences at Springer Nature 12 November 2022
- Best Paper Award at the In-Use Track ISWC 2022 12 November 2022
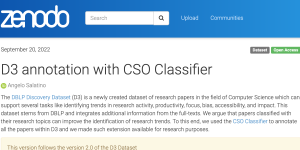
- Annotating D3 dataset with the CSO Classifier 20 September 2022
- Sci-K 2022 – International Workshop on Scientific Knowledge: Representation, Discovery, and Assessment 17 June 2022
- Enriching Data Lakes with Knowledge Graphs 17 June 2022
Tags
Bibliographic Data
big data
clique
Conference Proceedings
cso
data mining
data science
Digital Libraries
emerging topics
ffmpeg
graph
Knowledge Graph
Knowledge Graphs
Machine Learning
Matlab
Metadata
mksmart
mobility
Ontologies
Ontology
Ontology Learning
phd
podcasts
Qt Framawork
R
Research Dynamics
research topics
Research Trend Detection
Research Trends
Safety
Scholarly Communication
Scholarly Data
Scholarly Ontologies
science of science
semantic web
Semantic Web Technologies
sparql
Speech emotion recognition
springer
Text Mining
topic detection
Topic Discovery
Topic Emergence Detection
topic ontology
Word Embeddings