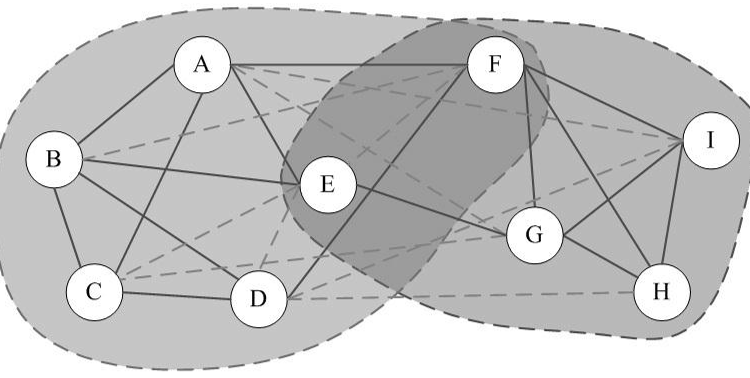
Clique Percolation Method (CPM) is an algorithm for finding overlapping communities within networks, introduced by Palla et al. (2005, see references). This implementation in R, firstly detects communities of size k, then creates a clique graph. Each community will be represented by each connected component in the clique graph.
Algorithm
The algorithm performs the following steps:
1- first find all cliques of size k in the graph
2- then create graph where nodes are cliques of size k
3- add edges if two nodes (cliques) share k-1 common nodes
4- each connected component is a community
Example with k=3
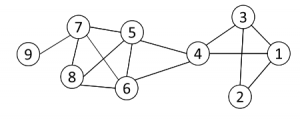
The presented graph contains the following cliques:
{1, 2, 3} {1, 3, 4} {4, 5, 6} {5, 6, 7} {5, 6, 8} {5, 7, 8} {6, 7, 8}
Each clique will represent a node in the clique graph and those node are connected each other if they share k-1 (2 in this case) nodes.
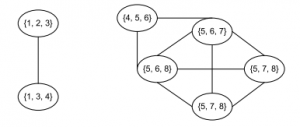
As a result, the clique graph presents two connected components containing {1,2,3,4} and {4,5,6,7,8}. The node 4 belongs to both communities. In other words, the graph contains two overlapping communities.
Description
Usage
- clique.community(graph, k) : Basic implementation with some bug fix from an old version (see section Bug Fix)
- clique.community.opt(graph, k) : Optimized version with reduction of search space (see section Optimizations)
- clique.community.opt.par(graph, k): Optimization via parallelization (see section Optimizations)
Arguments
- graph: the input graph (igraph object)
- k: the size of the clique (usually = 3)
Values
- memberships: an object containing list of communities
Package Dependencies
This implementation requires the following packages:
install.packages("igraph")
install.packages("doParallel")
install.packages("foreach")
Implementation, bug fix and optimisations
An old and rather inefficient implementation of this algorithm can be found here: http://igraph.wikidot.com/community-detection-in-r#toc0. However, this implementation contains couple of bugs, related to some updates of the library and it has room for an optimisation.
Bug Fix
1) Non-negative Vertex Id
Since version 0.6, vertices and edge are indexed from one in R iGraph and then that implementation produces the following error:
Error in .Call("R_igraph_create", as.numeric(edges) - 1, as.numeric(n), :
At type_indexededgelist.c:117 : cannot create empty graph with negative number of vertices, Invalid value
In addition: Warning message:
In max(edges) : no non-missing arguments to max; returning -Inf
Called from: .Call("R_igraph_create", as.numeric(edges) - 1, as.numeric(n),
as.logical(directed), PACKAGE = "igraph")
This issue has been now fixed.
2) Clique-Graph
In the same old implementation, the graph was created using the edge list: clq.graph <- simplify(graph(edges)) and then simplified. However, when performing the clique() function, some isolated cliques may appear (cliques that do not share k-1 nodes with others cliques). Relying on the previous version, isolated cliques and therefore cliques without any edge do not appear in the final computed clique graph. In some extreme cases, when the edges structure is empty (every clique is not connected with others), the algorithm generates the following error:
Error in .Call("R_igraph_create", as.numeric(edges) - 1, as.numeric(n), :
At type_indexededgelist.c:117 : cannot create empty graph with negative number of vertices, Invalid value
In addition: Warning message:
In max(edges) : no non-missing arguments to max; returning -Inf
Called from: .Call("R_igraph_create", as.numeric(edges) - 1, as.numeric(n),
as.logical(directed), PACKAGE = "igraph")
In this new version, clique.community.R, the graph is created inserting the right amount of vertexes and then all the edges. In this way, we avoid to lose nodes (cliques without edges), that can represent communities.
Optimizations of the Algorithm
The most computationally expensive section in the algorithm is the clique-graph creation process. It performs an extensive search on the space of cliques, looking for couples that share k-1 nodes. In the basic implementation (clique.community.R) there are two nested for loops comparing cliques and then performing n*n iterations.
Reduction of the Search Space
clique.community.opt.R implements an optimised approach to discover couples of cliques in the search space. As already mentioned the algorithm performs an exhaustive search of couples that share k-1 nodes. The two nested for loops over the same list of cliques correspond to a symmetric matrix-based search space that can be reduced in investigating either the upper or lower part. This implementation therefore reduces the number of iterations to n*(n-1)/2.
Parallelisation
Another implementation of the algorithm can be found in clique.community.opt.par.R. This implementation parallelises the research of couples of cliques exploiting the number of cores that nowadays CPU have at their disposal. In addition, it also implements the previous optimisation. To run, this implementation requires the foreach and doParallel packages and the number of clusters (parallel session of R) to parallelise the execution need to be defined at priori by the user. They can be defined using the following code:
cl <- makeCluster(4) #test on 4 cores
registerDoParallel(cl)
getDoParWorkers()
Results
Using the Zachary network as a benchmark, and running the three implementations on a Processor Intel(R) Core(TM) i7-3630QM CPU @ 2.40GHz, 2401 Mhz, 4 Core(s), 8 Logical Processor(s), it is possible to compare the elapsed of the different implementations:
> g <- make_graph("Zachary") #the karate network
> #Execution of the different implementation of the algorithm
> ptm <- proc.time()
> res1<-clique.community(g,3)
> proc.time() - ptm
user system elapsed
3.47 0.02 3.49
> ptm <- proc.time()
> res2<-clique.community.opt(g,3)
> proc.time() - ptm
user system elapsed
1.78 0.00 1.78
> ptm <- proc.time()
> res3<-clique.community.opt.par(g,3)
> proc.time() - ptm
user system elapsed
0.06 0.00 0.09 Project info
Github repository: https://github.com/angelosalatino/CliquePercolationMethod-R
Issue tracker: Here
References
Palla, G., Derényi, I., Farkas, I., & Vicsek, T. (2005). Uncovering the overlapping community structure of complex networks in nature and society. Nature, 435(7043), 814-818.